Percentile

What is it? Why is it used? And why is it important in the context of optimization and reliability engineering? Bonus: a browser app that lets you play with data.

In simple terms, we can think of a metric as an array of values with a timestamp and some optional tags.

For example, the latency metric values for an API endpoint may look like this:

metric_data = [
{ epoch: 1716898141, 200, tags: [ “api”, “GET” ] },
{ epoch: 1716898142, 212, tags: [ “api”, “GET” ] },
{ epoch: 1716898143, 102, tags: [ “api”, “GET” ] },
{ epoch: 1716898144, 290, tags: [ “api”, “GET” ] },
{ epoch: 1716898145, 180, tags: [ “api”, “GET” ] },
{ epoch: 1716898146, 3000, tags: [ “api”, “GET” ] },
{ epoch: 1716898147, 153, tags: [ “api”, “GET” ] },
…
]

Let’s ignore the timing and tags for now to focus on the values:

metric_values = [ 200, 212, 102, 290, 180, 3000, 153, … ]

In this dataset, most latency values are in the range [100ms..200ms] but there’s an outlier there: 3000ms. What happened there? Before we look into that, let’s see if one of the most common tools can help: average.

The average of the whole dataset including the outlier is:

average([200, 212, 102, 290, 180, 3000, 153]) = 591ms

Without the outlier we have:

average([200, 212, 102, 290, 180, 153]) = 189.5ms

So, it is 591ms versus 189.5ms! Pretty large difference!

That is how average works: it hides those outliers and makes all data look equally bad.

Average often does not represent an actual data point.

For example, the average American family has 1.94 children! I know what one child looks like, but what exactly is 0.94 child? 👶And apparently all families have it! 😄Even the ones with no kids! 🤯

If we want to focus our optimization efforts on the outliers, we need a tool that’s better than average (no pun intended)! We want a tool that picks actual outlier data points.

Say hello to percentiles!

Percentiles

Percentile is the value above a percentage of all data points.

OK, that was a mouthful. 🤭Let’s say we have a metric with these values:

These are 1000 values for a metric that is mostly hovering around 11000 to 12000 but occasionally there are outliers which are significantly higher or lower.

The purpose of percentiles is to find outliers.

The idea is very simple and intuitive:

1. Sort the data

2. Pick the data at the index that is at p% of the number of data points

Let’s try that with the dataset above.

1. The sorted data looks like this:

2. The percentile P0, P1, P2, …, P100 look like this:

Do you spot the similarity? That’s because percentiles are directly deduced from the sorted data points.

Note: for consistency, in this article we only sort the data in ascending order, but the data may as well be sorted in descending order. The sorting order is not a requirement for percentiles.

Now we can write a small function that returns a given data point at a desired percentile:

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

Show hidden characters

	/**
	* Gets the index of the element in an array that corresponds to the given percentile
	* @param {number} arrLength the length of the array that we want to calculate its percentile
	* @param {number} p the percentile in the range [0..100] inclusive
	* @returns index of the array element that corresponds to the given percentile
	*/
	export function percentileIndex(arrLength, p) {
	const maxPossibleIndex = arrLength - 1
	return Math.ceil(maxPossibleIndex * p / 100)
	}
	/**
	* @returns the value at the nth location in the array where n is between 0 to array.length
	*/
	export function percentile(arr, p) {
	return arr[percentileIndex(arr.length)]
	}

view raw percentile.js hosted with ❤ by GitHub

The code is pretty simple. It just returns the array element at the nth position where n is at the p% position of the array length.

Example:

• If the array has 100 elements, P99 is the item at the 99th position. For languages that start the array from 0, that would be arr[98]

• If the array has 1000 elements, P99 is the 990th element or arr[989]

• If the array has 24 elements, P95 is the 23rd element or arr[22]. That’s because the maximum possible array index is 23 and 95%23 = 21.85. Math.ceil(21.85) = 22. Since this array is so short, even P99 is also at arr[22].

In simple terms, P99 is the value that shows up at the 99% position in a sorted array.

While P99, P95, or even P90 are most used, there’s no rule that excludes other numbers between 0-100.

For example, if you want to find unusually small numbers in a dataset, you can look for P1 or even P0.1.

P0.1 may look confusing, but it uses the same rules as before: find the data at the 0.1% of the sorted dataset.

Example:

• If the array has 100 elements, P0.1 is the item at the 2nd position. For languages that start the array from 0, that would be arr[1]

• If the array has 10000 elements, P0.1 is the 11th element or arr[10]. That’s because the maximum possible array index is 9999 and 0.1%9999 = 9.999. Math.ceil(9.999) = 10.

Other notable percentiles are:

• P10: Also known as 1st Decile

• P20: Also known as 2nd Decile

• P25: Also known as 1st Quartile

• P50: Also known as median or 2nd Quartile (this is not the average, but the item that is located exactly in the middle of the array)

• P75: Also known as 3rd Quartile

• P80: Also known as 8th Decile

P50 is an interesting one. Instead of average, it represents the data in the middle of a sorted array.

For example, although the average American has 1.89 children, the median family has either 0, 1, or 2 children. I couldn’t find the stats in a way that allowed me to calculate the median, but you get the point: percentile selects a data point from the array whereas average aggregates the data points.

You don’t have to care about decile and quartile. I just wrote about them for the sake of inclusivity. In practice we almost exclusively work with percentile.

For the exact dataset that was visualized in this page, we have the following stats:

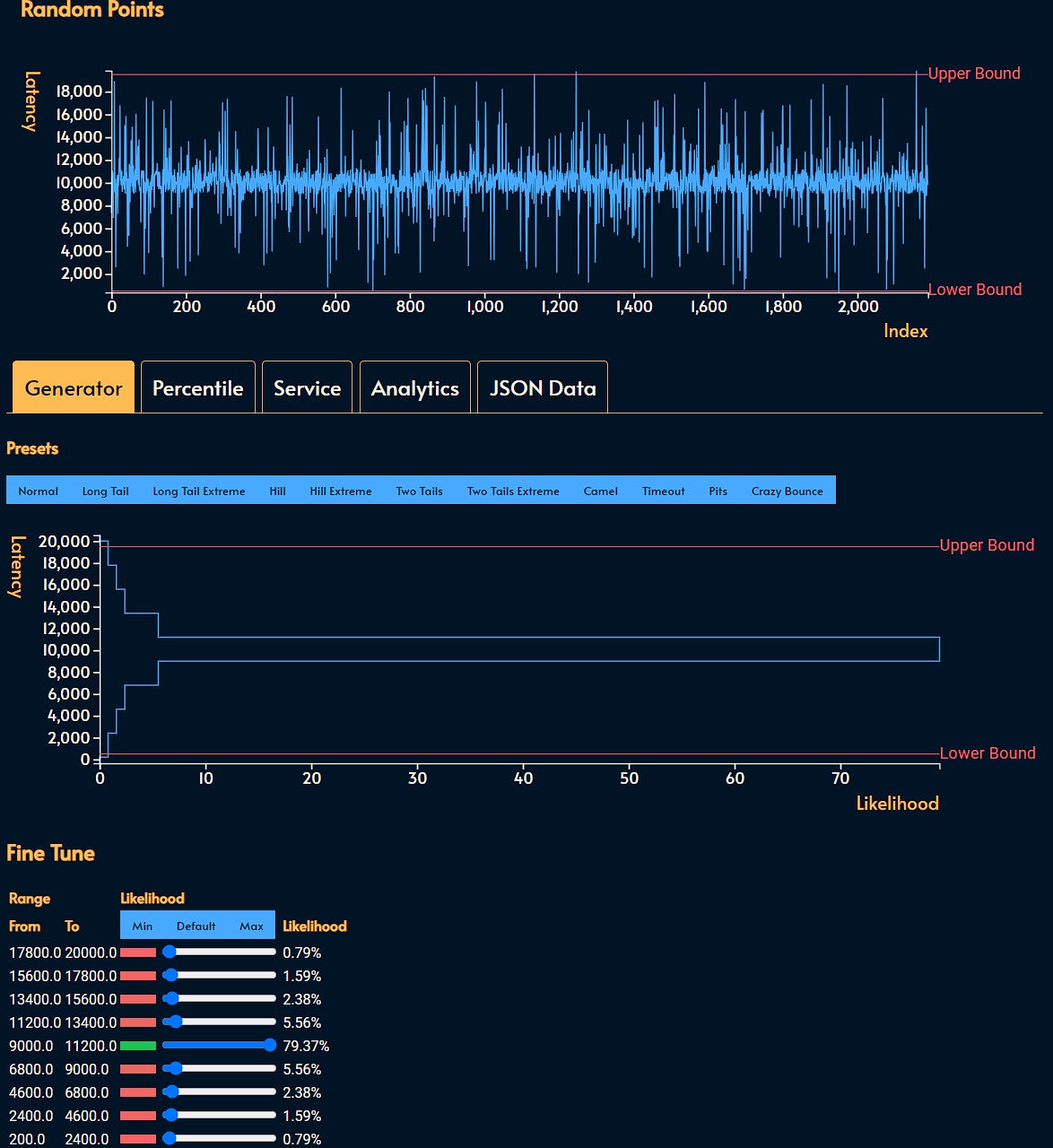
If you want to play with different datasets, I’ve written a free open-source tool that helped me learn and visualize these concepts.

The interface is a bit crud at the moment, but I have big plans for integrating it to the Service Leval Calculator.

Introducing Service Level Calculator

Note: using percentiles simplifies talking about data. For example, if you read:

12% of European households have 3 or more children —elfac.org

You know that if there was an array representing the number of children for each individual family in Europe:

• If it was sorted in the decreasing order, the family at the position P12, would have exactly 3 children

• If it was sorted in increasing order, the P88 family would have exactly 3 children.

When to use percentiles?

Percentile is a popular tool in the field of reliability engineering and performance optimization. It is a powerful tool to spot the outlier data points without diluting the story that a dataset is capable of telling.

Percentile is especially useful for datasets that are not evenly distributed —most data!

Evenly distributed what? —you may ask!

First let’s look at some evenly distributed data where each value is as likely to show up:

This is how random number generators work. In fact, this data was created using Math.random() in JavaScript as we’ll see later.

If we sort that data it we get this:

As you can see, there are no anomalies. If we do the math, we can see that:

• Mean (also known as average) is 10279

• Median (also known as P50 percentile) is 10453

Not an enormous difference considering that the range of values is anywhere from 0 to 20000. And that’s expected from such an evenly distributed dataset.

But the story is different when there are outliers.

For example, if a small fraction of numbers are unusually high, we get something like this:

Sorted, we get this:

• Mean (average): 2360

• Median (P50): 2106

• P95: 3969

• P99: 18031. This means 99% of values are below 18031

This type of data distribution is also known as long tail.

Another example where most values are high, but a few are very low:

Look for those extremely low values. They are easier to see when the data is sorted:

Analysing:

• Mean (average): 17556

• Median (P50): 18695

• P1: 2359. This means only 1% of values are below 2359.

• P99: 19969

And of course, there can be datasets where most data fluctuate around a usual range, but occasionally there are outliers that are either too high or too low:

Sorted:

Analyzing:

• Mean (average): 10048

• Median (P50): 10076

• P1: 1546

• P99: 17949

• P99.5: 18858

• P99.9: 19378

Selection vs aggregation

Percentile can select a subset of actual data to analyze and drive meaningful action.

For example, let’s say you are a policy maker who wants to reduce child obesity in Belgium. According to statista 5.2% of Belgian children are obese. That’s a tiny number and if we were going to use average weight, we would think that the average Belgian child is slightly obese. Considering that a percentage of the children may be underweight, the average may actually mislead us to believe that the average Belgian child has a perfectly healthy BMI (body mass index).

However, if we sort all Belgian kids in a very very long row based on their BMI, we can quickly identify the obese ones.

This allows you to focus on one end of the row where obese children are standing and trying to understand what contributes to their obesity and what policies can reduce their risk factors.

Crazy bounce

One final tip: when starting to optimize the system behavior, start from the common percentiles (e.g. P50) and gradually shrink your focus towards the outliers (e.g. P1 or P99 depending on the shape of the sorted diagram).

There is, however, no universal rule. Always start by looking at the sorted data to understand where you want to start.

For example, this rather uncommon dataset fluctuates between very high and very low values:

Sorted:

As you can see, the majority of data points are either too low or too high. This might be the average latency of an API where the data from GET and POST requests are combined in one view.

Here, you may want to use labels to narrow down the dataset to something that P1 or P99 can meaningfully tell a story and direct our optimization.

For example, we may realize that if we only look at the data for GET requests to the API, we see a long tail diagram like the ones we saw before. And that may actually look quite good. Maybe, it is the PUT requests that are taking too long.

Different subsets of data may tell different stories which may drive different actions.

Recap

Percentiles allow:

• Selecting the outliers and focusing on understanding them (instead of aggregating them as average does)

• Focusing the optimization efforts

• Impactful decisions that are guided by actual data points

Start the optimization effort with a percentile that represents the typical data points. As your optimization yields results, narrow down your efforts to more niche outliers.

There is no universal rule that applies to all datasets. The best way to know which percentile to use is to look at the sorted data.

You may have to filter the data to get to a shape that is actionable.

Try to identify the actions with the best ROI (return on investment). Just because there is a long tail, doesn’t mean that you have to trim it! 🐍

---

My monetization strategy is to give away most content for free. However, these posts take anywhere from a few hours to days to draft, edit, research, illustrate, and publish. I pull these hours from my private time, vacation days and weekends. Recently I went down in working hours and salary by 10% to be able to spend more time sharing my experience with the public. You can support this cause by sparing a few bucks for a paid subscription. As a token of appreciation, you get access to the Pro-Tips section as well as my online book Reliability Engineering Mindset. Right now, you can get 20% off via this link. You can also invite your friends to gain free access.