Composite SLO

How to calculate the SLO of a complex system that is made of multiple components?

Complex systems are made of many components. We may have a Service Level Objective (SLO) for each component but how do we calculate the SLO for the entire system?

For example, if you have 4 replicas of a microservice, how exactly does it improve the reliability of the whole?

Or if a system can only function if all its dependencies are functioning, how do we calculate the reliability of that system?

System engineering has two simple rules for calculating composite SLO:

• Multiply SLOs for serial dependencies

• Multiply error budgets for parallel dependencies

Both use a basic concept in probability theory:

\(P(A \cup B) = P(A).P(B)\)

The probability of two independent events happening at the same time is the result of multiplying the probability of each one happening individually.

Let’s unpack that with plenty of examples.

Note: composite SLO is about how to calculate the SLO of different sub-systems in a complex system. It’s not to be confused with multi-tiered SLO which is about having multiple SLOs for the same system.

Serial Dependencies

In the diagram below, we have 3 systems:

System A has a serial dependency to Systems B and C (tight coupling)

System A: an API that has two hard dependencies

1. System B: a database with the availability of 99.8%

2. System C: an upstream API with the availability of 95.3%

Looking at the uptime of those systems we can see that system A is only available when its dependencies are available:

If any dependency fails, our system fails too

Note: This is a simplified example. The code in system A can also fail which may make it unavailable even if its dependencies are available. Also, system A may be running on an infrastructure reling on networks, operating systems, hardware, and configuration that may fail. We also assumed that System B and System C could fail independently. In reality, they may both run on the same infrastructure which acts as a serial dependency for those systems (i.e., when the infra fails, all the systems that run on it fail as well).

As we can see, the probability of System A being available equals to the probability of System B and C being available.

SLO is expressed in percentage, but we use numbers in the 0 to 1 range when using probability math:

1. Probability of system B being available: 0.998

2. Probability of System C being available: 0.953

Probability of System A being available = 0.998 x 0.953 = 0.951094

Expressed in percentage, the SLO of System A is 95.1094%

As you can see, the availability of System A is worse than its least reliable dependency, which is expected in the case of serial dependency.

Parallel Dependencies

In the diagram below, we have 3 systems:

System A has a parallel dependency to Systems B and C (loose coupling)

System A: an API gateway that has two parallel dependencies:

1. System B: an upstream in the local region with the availability of 99.8%

2. System C: the same upstream in another region with the availability of 95.3%

We picked the same numbers as before just to see how serial and parallel dependencies impact the overall system reliability.

Looking at the uptime of those systems we can see that system A is available when either System B or C are available:

Our system only fails when both dependencies fail at the same time.

As we can see, the probability of System A being unavailable equals to the probability of System B and C being unavailable.

Converting SLO percentage to the 0 to 1 range to make them suitable for probability math we have:

1. Probability of system B being unavailable: 1 - 0.998 = 0.002

2. Probability of System C being unavailable: 1 - 0.953 = 0.047

Probability of System A being unavailable = 0.002 x 0.047 = 0.000094

Converting it to the percentage, we get 0.0094% but that is unavailability (i.e. the error budget). The SLO will be the complement of that:

System A availability = 100% - 0.0094% = 99.9906%

As you can see, the availability of System A is better than its most reliable dependency, which is expected in the case of parallel dependency.

More Complex and Realistic Example

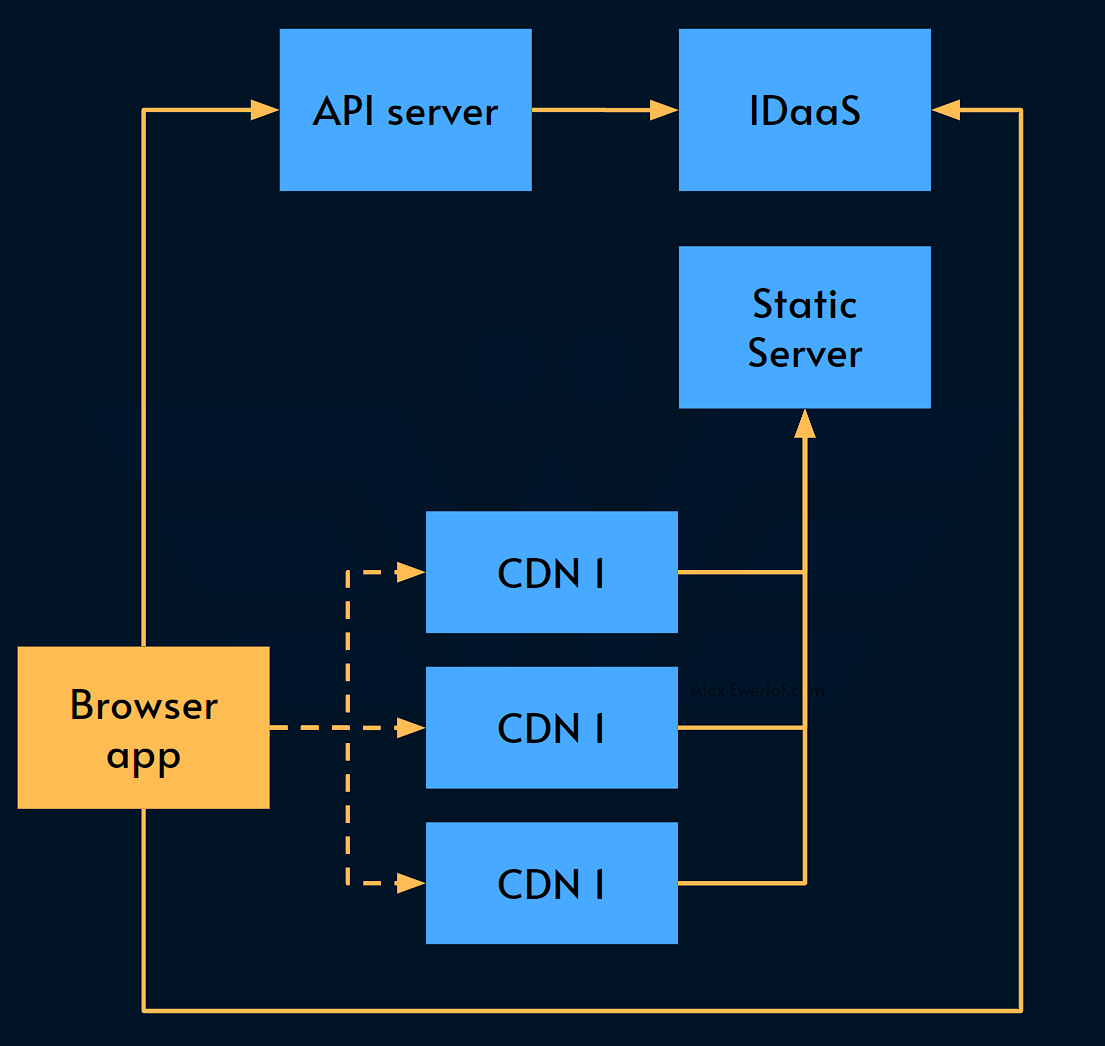
This is a typical website example:

• Static server serves the website assets like HTML, JavaScript, CSS, images, etc. This simple service is run behind CDN which is available from multiple locations

• CDN: Content Delivery Network distributes static files across the globe. CDN usually has a cache that acts as a fallback mechanism for when the upstream server is down. This CDN also has a failover mechanism to automatically pick the next node when one of the nodes is down.

• API server: supports the functionality of the web app. For example, it can be a BFF (dedicated backend for frontend), or a GraphQL server abstracting away multiple other APIs toward the browser application.

• IDaaS: The website and API server both depend on a 3rd party identity as-a-service provider.

Based on the research, you get the following availability numbers:

• The CDN provider commits to 99.9% availability for each of their edge nodes

• The IDaaS provider commits to 99% availability in their SLA

• The static file server is available 98% of the time based on historical data

• The API server is available 95% of the time. That is because the API server has hard dependencies to other upstream services which are not shown in the diagram.

So how do we go about calculating the availability of the browser application?

It has 3 dependencies:

• CDN is available if any of its 3 nodes are available.

  • Each CDN node has a serial dependency on the static server. Therefore, the usefulness of the CDN node is 0.999 x 0.98 = 0.97902. This means the error budget for each CDN node is 1 - 0.97902 = 0.02098

  • There are 3 CDN nodes in parallel, so the collective error budget is calculated from multiplying their error budgets: 0.02098 x 0.02098 x 0.02098 = 0.00000923456

  • Therefore, the availability of the CDN is 1 - 0.00000923456 = 0.99999076544

  • The whole CDN (including the 3 nodes) can be seen as one serial dependency for the browser app.

• API server is available 95% but since it also requires the IDaaS provider to serve the browser, its availability is 0.95 x 0.99 = 0.9405

• IDaaS is available 99% towards the browser too. Converted to 0-1 range, we get 0.99

Putting them all together, the browser app’s availability is the multiplication of all its serial dependencies for it to be served, function, and identify the user:

0.99999076544 x 0.9405 x 0.99 = 0.93108640174

Converted to percentage, we get 93.108640174% or 93.1% for short.

Is it good? Is it bad? It really depends on what makes sense to your service consumers as we discussed in “lagom” SLO:

Lagom SLO

Pro-Tips

My monetization strategy is to give away most of content for free. However, these posts take anywhere from a few hours to days to draft, edit, illustrate, and publish. I pull these hours from my private time and weekends. For those who spare a few bucks, the pro-tips are a token of appreciation. The bar for pro-tips is to give tools and mindset that you can use at your work to earn more. Right now, you can get 20% off via this link. If you don’t want to spend money, sharing it with a wider audience also helps. Thanks in advance.